¶ Extending Cellular Automata
A common practice to make progress with particularly intractable engineering problems involves extending the numerical domain of the model under consideration to take into account not only the ‘Real’ numbers, but also the ‘Imaginary’ numbers. The so-called ‘complex’ numbers offer a larger dimensional space with which to embed traditional 1D Cellular Automata.
The key idea being explored here is to carefully consider the implications of assuming that nearest-neighbor Cellular Automata (i.e. 'Left', ‘Center’, ‘Right’ Cells) can be modeled in a higher dimensional space consisting of an additional dimension which provides for new neighbor interactions (i.e. ‘Up’, ‘Center’, ‘Down’).
It turns out that such an extended space readily exists, and can be represented and visualized by Voxels.
¶ Voxel Axes Definitions
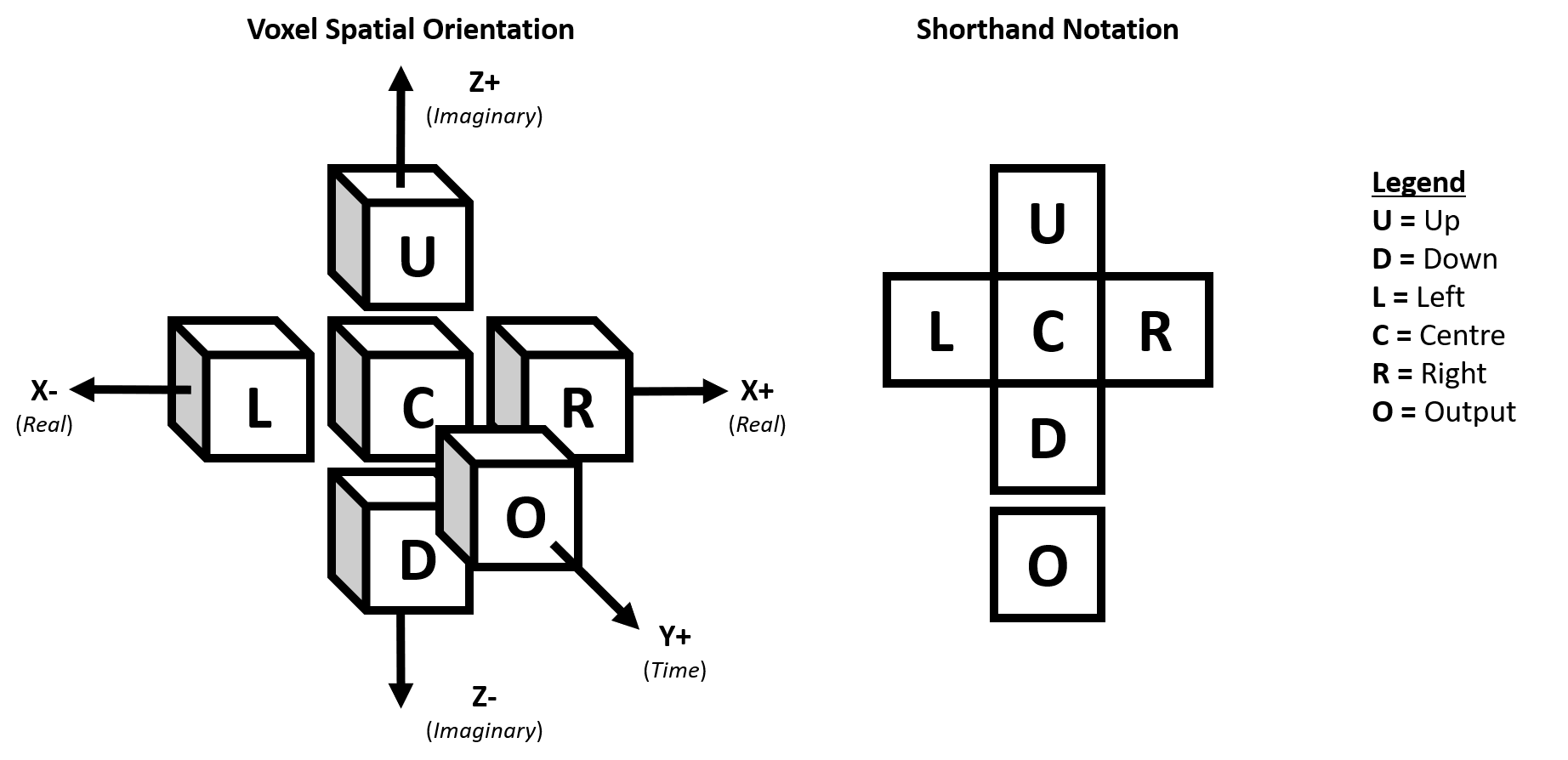
¶ Notes:
- The Y-Axis is interpreted as the VA evolution over time.
- A cell undergoing evolution in time persists as the ‘Center’ cell.
- The X-Axis is defined as the Left-Right axis.
- The Z-Axis is defined as the Up-Down axis.
- The X-Axis is analogous to the ‘Real’ number line.
- The Z-Axis is analogous to the ‘Imaginary’ number line.
- The X-Y plane (At Z=0) is defined to be equivalent to the traditional 1D cellular automata (CA) plane.
- The Z-Y plane (At X=0) is defined to be analogous to an "Imaginary plane" orthogonal to the traditional 1D CA plane.
- The X-Z plane is analogous to the ‘Complex’ number plane.
¶ Voxel Automata Enumeration
The shorthand ‘tile’ notation shown below is used to illustrate all cell state input combinations of a cell and it's nearest-neighbors, along with the associated cell output state for the next step of evolution.
¶ Example VA rule:
| Binary | 0001 1110 0000 1111 0000 1111 0001 11102 |
| Hexadecimal | 1E0F 0F1E16 |
| Decimal | 504,303,39010 |
¶ Example: Tiles for VA rule 504,303,39010
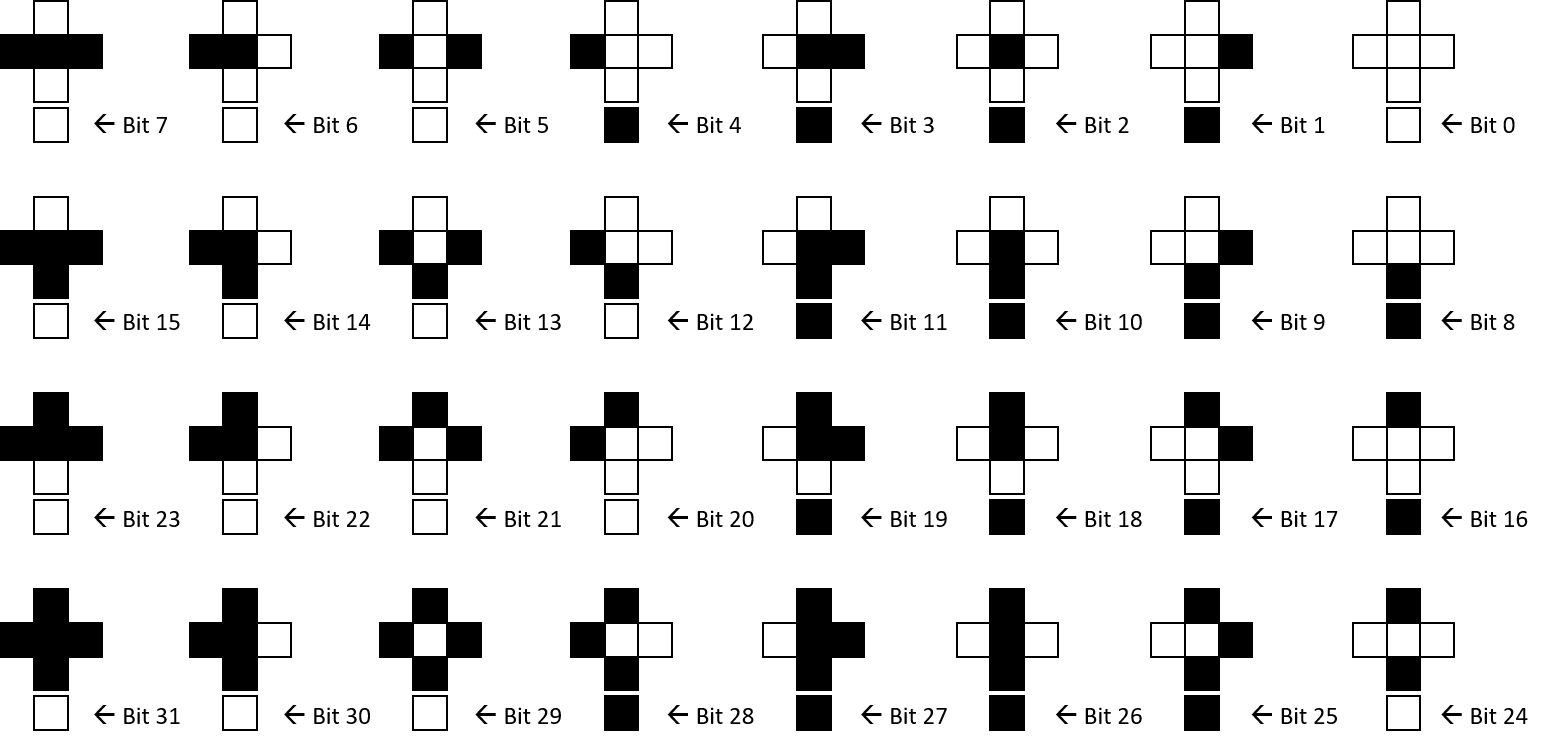
¶ Notes:
- The method replicates that which is commonly used to enumerate Cellular Automata.
- Only immediate Up, Down, Left, and Right cells are considered neighbors to the Center cell.
- A total of 3210 (= 25) unique input combinations exist when taking into account the cell state plus nearest-neighbors.
- The Output cell (O) is illustrated below the tile, and represents the cell state on the next step of evolution.
- The binary digit sequence defined by the output bit pattern forms the ‘VA rule’ number.
- VA codes range from 0 to 4, 294, 967, 29610 (= 232), inclusive.
¶ Example: Bit pattern for VA Rule 504,303,39010
| U | D | L | C | R | O | ||
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | ← Least significant output bit | |
| 0 | 0 | 0 | 0 | 1 | 1 | ||
| 0 | 0 | 0 | 1 | 0 | 1 | ||
| 0 | 0 | 0 | 1 | 1 | 1 | ||
| 0 | 0 | 1 | 0 | 0 | 1 | ||
| 0 | 0 | 1 | 0 | 1 | 0 | ||
| 0 | 0 | 1 | 1 | 0 | 0 | ||
| 0 | 0 | 1 | 1 | 1 | 0 | ||
| 0 | 1 | 0 | 0 | 0 | 1 | ||
| 0 | 1 | 0 | 0 | 1 | 1 | ||
| 0 | 1 | 0 | 1 | 0 | 1 | ||
| 0 | 1 | 0 | 1 | 1 | 1 | ||
| 0 | 1 | 1 | 0 | 0 | 0 | ||
| 0 | 1 | 1 | 0 | 1 | 0 | ||
| 0 | 1 | 1 | 1 | 0 | 0 | ||
| 0 | 1 | 1 | 1 | 1 | 0 | ||
| 1 | 0 | 0 | 0 | 0 | 1 | ||
| 1 | 0 | 0 | 0 | 1 | 1 | ||
| 1 | 0 | 0 | 1 | 0 | 1 | ||
| 1 | 0 | 0 | 1 | 1 | 1 | ||
| 1 | 0 | 1 | 0 | 0 | 0 | ||
| 1 | 0 | 1 | 0 | 1 | 0 | ||
| 1 | 0 | 1 | 1 | 0 | 0 | ||
| 1 | 0 | 1 | 1 | 1 | 0 | ||
| 1 | 1 | 0 | 0 | 0 | 0 | ||
| 1 | 1 | 0 | 0 | 1 | 1 | ||
| 1 | 1 | 0 | 1 | 0 | 1 | ||
| 1 | 1 | 0 | 1 | 1 | 1 | ||
| 1 | 1 | 1 | 0 | 0 | 1 | ||
| 1 | 1 | 1 | 0 | 1 | 0 | ||
| 1 | 1 | 1 | 1 | 0 | 0 | ||
| 1 | 1 | 1 | 1 | 1 | 0 | ← Most significant output bit |